解説:設問の条件では線間電圧が与えられているが、計算上、1相あたりの相電圧で考えてから最終的に線間電圧に変換する方が考えやすいので、その方針で解いていく。
送・受電端電圧①の通り、送電端相電圧を$\dot{E_s}$[V] , 受電端相電圧を$\dot{E_r}$[V] , 線電流を$\dot{I}$[A], 負荷力率角をθ, 送電端相電圧と受電端相電圧の相差角をδ, 1相あたりの線路リアクタンスをX[Ω]とした時、受電端相電圧$\dot{E_r}$[V]を基準にした時のベクトル図は下図の様になる。
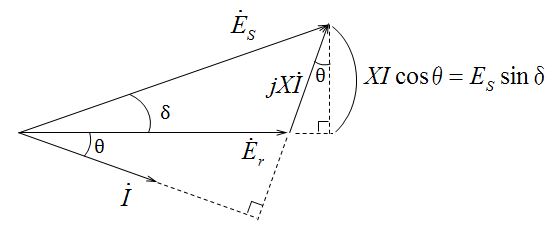
図中の線分abの大きさは、線路リアクタンスによる電圧降下から目線ではXIcosθであり、送電端相電圧目線では$E_s$sinδである。いずれも同一線分abの大きさを表しているので、
XIcosθ=$E_s$sinδ・・・①
となる。
送電端相電圧$\dot{E_s}$[V]は受電端相電圧$\dot{E_r}$[V]と線路リアクタンスによる電圧降下$jX\dot{I}$[V]との和であるので、線路リアクタンスの分だけ無効電力を供給し、受電端よりも高い電圧を送電する必要があるが、有効電力は送電端も受電端も等しい。
1相あたりの有効電力を$P_1$とすると、
$P_1=E_r$Icosθ[W]・・・②
ここで、先ほどの①を利用して②へ代入すると、
$P_1=$$\frac{E_sE_r}{X}sinδ$[W]
三相3線式での有効電力を$P_3$とすると、
$P_3=3P_1=$$\frac{3E_sE_r}{X}sinδ$[W]
ここで、相電圧を線間電圧に変換すると、$V_r=\sqrt{3}E_r , V_s=\sqrt{3}E_s$なので、
$P_3=$$\frac{V_sV_r}{X}sinδ$[W]