正解:(4)
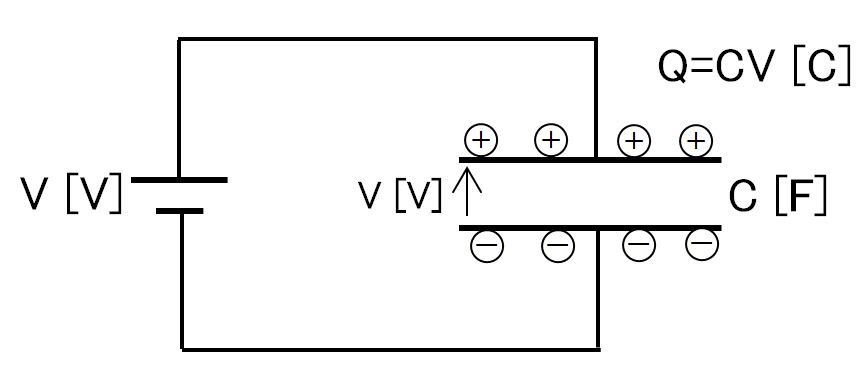
解説:図のように電圧が印加されたコンデンサには電荷が帯電し、コンデンサ間の電圧は印加された電圧に等しくなる。このとき、コンデンサに帯電する電荷は静電容量と電圧の積で表すことができ、Q=CV[C]となる。静電容量が大きい程、また電圧が大きい程、蓄えられる電荷量は大きくなる。
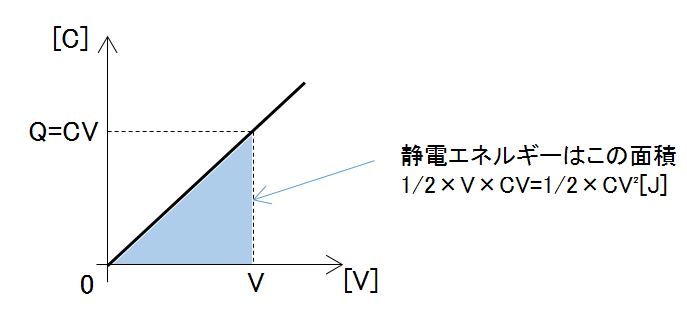
次に、グラフのように、電圧に対して蓄えられる電荷量が増えていくので、蓄えられた静電エネルギーは$\frac{1}{2}CV^2[J]$となる。
ここで気をつけたいのが、一様な電界中でQ[C]をV[V]だけ移動したときの仕事量はQV[J]となるが、コンデンサは電圧と共に電荷が増えるため、単純にQV=CV²としてはいけない。
イメージとしては、放電する時を考えると、最初の電荷はマックスの電圧で移動できるが、少しずつ放電していくと、電荷が減るため、電極間の電圧も小さくなり、徐々に電荷が移動する際の勢いが弱くなり、最終的には電圧が0になる。平均をとってその中間の1/2を掛ける感覚を持っていれば、単純に電荷Qに電圧Vを掛けてはなかないことが理解できる。