RLC平衡三相負荷（過去問にチャレンジ）解答

正解：(a)（２）、(b)（２）

解説

(a)：答えまでの方針は、負荷側をY形に変換し、1相あたりのインピーダンスを求め、力率が1より、インピーダンスの虚数部=0の方程式からL[H]を求めていく。

まずは、Δ－Y変換すると、Δ-Y変換③の様に、1相あたり抵抗Rと静電容量3C[F]のコンデンサの並列回路ができる。また、ここにL[H]のコイルが直列接続されているので、

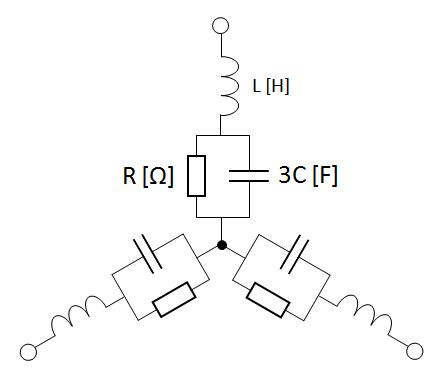
1相あたりのインピーダンスは、
$\dot{Z}=j\omega L+\frac{1}{\frac{1}{R}+j3\omega C}=j\omega L+\frac{R}{1+j3\omega RC}$$=j\omega L+\frac{R(1-j3\omega RC)}{1+9(\omega RC{)}^2}$
虚数部=0であるので、$\omega L+\frac{-3\omega R^{2}C}{1+9(\omega RC{)}^2}=0$より、$\omega L=\frac{3\omega R^{2}C}{1+9(\omega RC{)}^2}$したがって、$L=\frac{3R^{2}C}{1+9(\omega RC{)}^2}$となるので、正解は（２）

(b)：答えまでの方針は、(a)で求めた1相あたりのコンデンサ3C[F]と抵抗R[Ω]の並列回路に印加する電圧を求め、実際に問われているのは線間電圧であるので、√3倍して、答えを導く。

まず、1相あたりのインピーダンスは、(a)のうち虚数部=0なので、$\dot{Z}=\frac{R}{1+9(\omega RC{)}^2}$である。

この$\dot{Z}$に対する、コンデンサ3C[F]と抵抗R[Ω]の並列回路のインピーダンスの比により並列回路への印加電圧が分かる。また、相電圧はV/√3であるので、
$\frac{V}{\sqrt{3}}\times \frac{\frac{R}{1+j3\omega RC}}{\frac{R}{1+9(\omega RC{)}^2}}=\frac{V}{\sqrt{3}}\times (1-j3\omega RC)$
よって、電圧の大きさは、
$\frac{V}{\sqrt{3}}\times \sqrt{1+9(\omega RC{)}^2}$
最後に、√3を掛けて、
$V\times \sqrt{1+9(\omega RC{)}^2}$
したがって、正解は（２）

問題を選ぶ