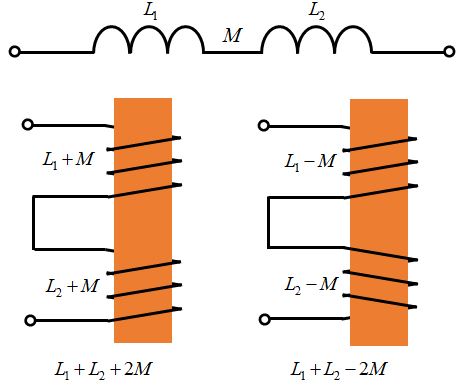
解説:回路図の様に自己インダクタンスL₁、L₂、相互インダクタンスMの2つのコイルを直列接続する時、それぞれのコイルの巻き方や接続方法によって、合成インダクタンスが変わる。①の巻き方と接続方法の場合、それぞれのコイルで発生する磁束が強め合う方向に働き、合成インダクタンスはL₁+L₂+2Mとなり、一方、②の巻き方と接続方法の場合、それぞれのコイルで発生する磁束が打ち消し合う方向に働き、合成インダクタンスはL₁+L₂-2Mとなる。
相互インダクタンスMの最大値はお互いの磁束が100%影響しあう時であり、
$M_{max}=\sqrt{L_1L_2}$
である。分かりやすくL₁=L₂=Lとするとき、
$M_{max}$=Lであり、合成インダクタンスの最大値はL+L+2L=4Lになる。
【ここで1つ疑問】
N巻でインダクタンスLのコイルを2つ使った場合、上記通り、合成インダクタンスが4Lになる。一方、2倍巻(2N巻)のコイルだと、実質はN巻のコイル2つよりも、むしろ1つのコイルとして完結しているのだからインダクタンスがより高いはずであるが、Lの2倍だから、2倍巻コイルのインダクタンス2Lとなり、N巻コイル2つの合成インダクタンスより小さい?なぜ?
→これは2倍巻コイルのインダクタンスを2Lと考えたのがそもそもの間違い。インダクタンスの通り、L[H]=N・$\frac{dΦ}{di}$であるので、LはNとΦに比例する。
また、磁束Φ=B[T]×S[m²]であり、半径aでN巻コイルの磁束密度はB=$\frac{μNI}{2a}$[T]であるため、磁束ΦもNに比例する。
つまり、インダクタンスL[H]は巻数Nの2乗に比例する。
したがって、巻数が2倍になったコイルのインダクタンスは4倍→4Lになるため、相互インダクタンスがMAX(100%)の時の合成インダクタンスと等しくなる。
簡単に言うと、コイル2つを合成して最大の合成インダクタンスを得たい場合には、1つのコイルとしてまとめてしまうのが良い。