正解:(3)
解説:電源電圧と抵抗に印加される電圧、リアクタンスに印加される電圧のベクトル図を表すと下図のようになり、
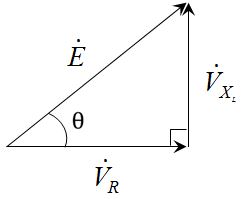
有効電力を担う抵抗の電圧に対して、無効電力のリアクタンス電圧は直交している。この抵抗とリアクタンスの電圧のベクトル和が電源電圧となる。
次に電圧の大きさ(ベクトルの大きさ)について考える。オームの法則(V=RI)を利用して、一旦ベクトルの方向について無視し、大きさだけを考えると、$|\dot{V}_R|=|\dot{I}|R$ , $|\dot{V}_{X_L}|=|\dot{I}|X_L$ , $|\dot{E}|=|\dot{I}||\dot{Z}|=|\dot{I}|\sqrt{R^2+{X_L}^2}$であるので、
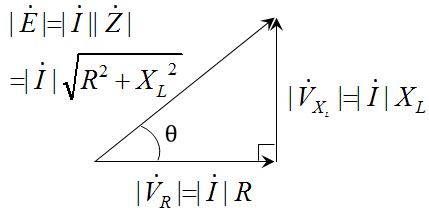
電圧の大きさの比は、
$E:V_R:V_{X_L}=I\sqrt{R^2+{X_L}^2}:IR:IX_L=\sqrt{R^2+{X_L}^2}:R:X_L$
である。これは、抵抗とリアクタンスの値が分かり、抵抗orリアクタンスor電源電圧のいずれか1つの電圧の大きさが分かることで、その他の電圧の大きさが分かることを意味する。
したがって、今回の設問では電源電圧が与えられ、残る抵抗とリアクタンスに印加する電圧の大きさを求めるので、
$V_R=\frac{R}{\sqrt{R^2+{X_L}^2}}E$
$V_{X_L}=\frac{X_L}{\sqrt{R^2+{X_L}^2}}E$
である。したがって、(3)が正解。
抵抗同士の直列回路では単純に抵抗の比をとれば良かったが、今回のように抵抗とリアクタンスのように、印加電圧が直交するケースでは電圧の比に三平方の定理を絡めて整理していく。