RL回路（並列回路の電流）解答

正解：（２）

解説：並列回路へ印加される電圧は等しいので、10[Ω]の負荷と、4+j3[Ω]の負荷にはそれぞれ50∠0°[V]の電圧が印加される。10[Ω]へ流れる電流をI₁とすると、オームの法則より、 $| \dot{I_{1}} |$ =50∠0÷10=5[A]。また、4+j3[Ω]へ流れる電流をI₂とすると、オームの法則より、 $| \dot{I_{2}} |$ =50∠0÷(4+j3)=50÷5(cosθ+jsinθ)=10(cosθ-jsinθ)[A]。ここで4+j3のなす角θは図のような関係であるので、

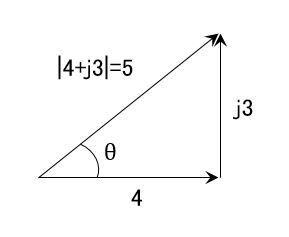
cosθ=0.8、sinθ=0.6であり、これを $| \dot{I_{2}} |$ =10(cosθ-jsinθ)に代入して、 $| \dot{I_{2}} |$ =10(0.8-0.6)=8-j6[A]。回路全体に流れる電流は $| \dot{I_{1}} |$ と $| \dot{I_{2}} |$ の和であるので、 $| \dot{I} | = | \dot{I_{1}} | + | \dot{I_{2}} | = 5 + (8 - j 6) = 13 - j 6 [A]$ となる。求めるのは、電流の大きさであるので、

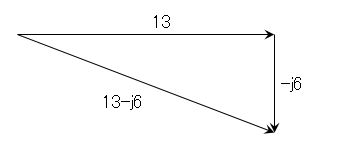
$| \dot{I} | = \sqrt{13^{2} + 6^{2}} = \sqrt{169 + 36} = \sqrt{205} ≒ 14.3 [A]$ 。

問題を選ぶ