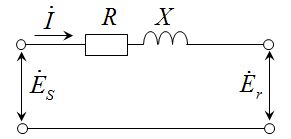
送電端相電圧を$\dot{E}_s$[V] , 受電端相電圧を$\dot{E}_r$[V] , 線電流を$\dot{I}$[A], 負荷力率角をθ, 1相あたりの線路抵抗をR[Ω]、1相あたりの線路リアクタンスをX[Ω]とした時、受電端相電圧$\dot{E}_r$[V]を基準にした時のベクトル図は下図の様になる。
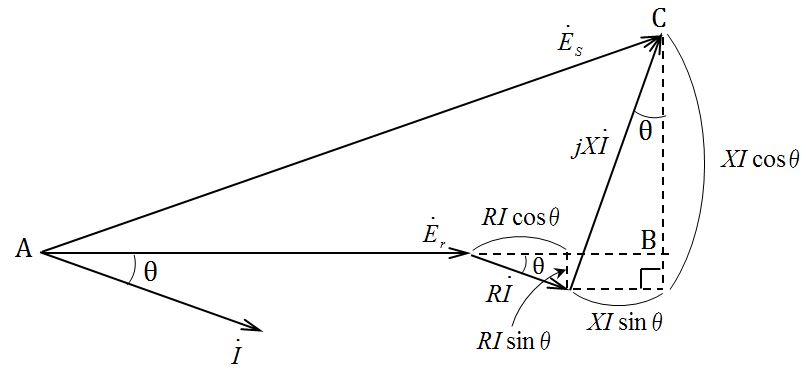
送電端相電圧$\dot{E}_s$の大きさは図中の線分ACの大きさであり、$AC=\sqrt{AB^2+BC^2}$であるので、
$E_s=\sqrt{(E_r+(ア)+(イ))^2+((ウ)-(エ))^2}$
一般的に線分BCは線分ABに比べて小さく、線分ACの大きさにあまり影響を及ぼさないので、AC≒ABとして近似して考えることができる。したがって、
$E_s=E_r+(ア)+(イ)$
送電線路1相あたりの電圧降下⊿Eは
⊿E=$E_s-E_r=(ア)+(イ)$
三相3線式の場合、相電圧を線間電圧に変換すると、$V_r=\sqrt{3}E_r,V_s=\sqrt{3}E_s$なので、線間電圧降下⊿Vは
⊿V=$V_s-V_r=(オ)((ア)+(イ))$
となる。
上記の記述中の空白箇所(ア)、(イ)、(ウ)、(エ)、(オ)に当てはまる組合せとして、最も適切なものを次の(1)~(5)のうちから一つ選べ。
| ア | イ | ウ | エ | オ | |
| (1) | RIcosθ | XIsinθ | RIsinθ | XIcosθ | 3 |
| (2) | RIcosθ | XIsinθ | XIcosθ | RIsinθ | $\sqrt{3}$ |
| (3) | RIsinθ | XIsinθ | RIcosθ | XIcosθ | $\sqrt{3}$ |
| (4) | RIsinθ | XIcosθ | XIsinθ | RIcosθ | $\sqrt{3}$ |
| (5) | RIsinθ | XIcosθ | RIcosθ | XIsinθ | 3 |