送・受電端電圧と電力①解答

正解：（２）

解説：送電端相電圧を $\dot{E_{s}}$ [V] , 受電端相電圧を $\dot{E_{r}}$ [V] , 線電流を $\dot{I}$ [A], 負荷力率角をθ, 送電端相電圧と受電端相電圧の相差角をδ, 1相あたりの線路リアクタンスをX[Ω]とした時、受電端相電圧 $\dot{E_{r}}$ [V]を基準にした時のベクトル図は下図の様になる。

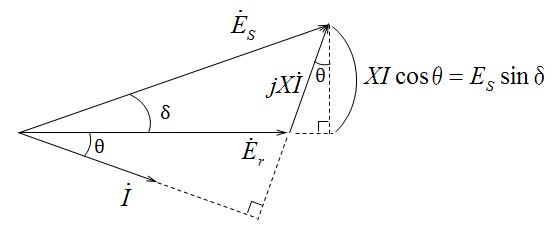
図中の線分abの大きさは、線路リアクタンスによる電圧降下から目線ではXIcosθであり、送電端相電圧目線では $E_{s}$ sinδであり、

XIcosθ＝ $E_{s}$ sinδ・・・①

となる。

送電端相電圧 $\dot{E_{s}}$ [V]は受電端相電圧 $\dot{E_{r}}$ [V]と線路リアクタンスによる電圧降下 $j X \dot{I}$ [V]との和であるので、線路リアクタンスの分だけ無効電力を供給し、受電端よりも高い電圧を送電する必要があるが、送電端有効電力と受電端有効電力は等しい。

1相あたりの有効電力を $P_{1}$ とすると、

$P_{1} = E_{r}$ Icosθ[W]・・・②

ここで、先ほどの①を利用して②へ代入すると、

$P_{1} =$ $\frac{E_{s} E_{r}}{X} s i n δ$ [W]

三相３線式での有効電力を $P_{3}$ とすると、

$P_{3} = 3 P_{1} =$ $\frac{3 E_{s} E_{r}}{X} s i n δ$ [W]

ここで、相電圧を線間電圧に変換すると、 $V_{r} = \sqrt{3} E_{r}, V_{s} = \sqrt{3} E_{s}$ なので、

$P_{3} =$ $\frac{V_{s} V_{r}}{X} s i n δ$ [W]

問題を選ぶ