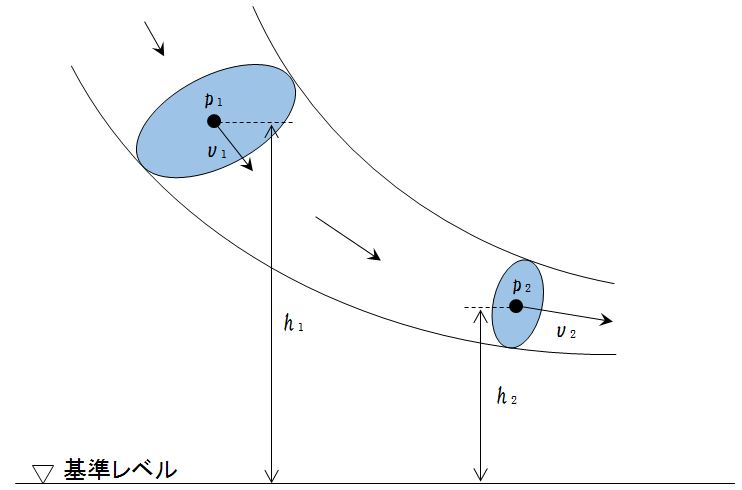
図のように水管中に流体が流れ、エネルギーの損失がない場合には、エネルギー保存の法則により(ア)エネルギーと(イ)エネルギーと(ウ)エネルギーの合計は水管中のどの場所でも一定となる。(ア)エネルギーをmgh、(イ)エネルギーを$m\frac{p}{ρ}$、(ウ)エネルギーを$\frac{1}{2}$mv²とすると、
$mgh+m\frac{p}{ρ}+\frac{1}{2}mv^2=一定$
図中の記号を適用すると、
$mgh_1+m\frac{p_1}{ρ}+\frac{1}{2}m{v_1}^2=mgh_2+m\frac{p_2}{ρ}+\frac{1}{2}m{v_2}^2=一定$
となる。この式の両辺をmgで割り、
$h_1+\frac{p_1}{ρg}+\frac{{v_1}^2}{2g}=h_2+\frac{p_2}{ρg}+\frac{{v_2}^2}{2g}=一定$
これをベルヌーイの定理という。
ただし、m:質量[kg]、g:重力加速度[m/s²]、ρ:流体の密度[kg/m³]、h:基準点からの高さ[m]、p:圧力[N/m²]、v:速度[m/s]とする。
上記の記述中の空白箇所(ア)、(イ)、(ウ)に当てはまる組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
| ア | イ | ウ | |
| (1) | 高さ | 重力 | 速度 |
| (2) | 位置 | 重力 | 速度 |
| (3) | 高さ | 圧力 | 速度 |
| (4) | 位置 | 圧力 | 運動 |
| (5) | 高さ | 圧力 | 運動 |