地絡故障計算①解答｜電験3種1問1答

正解：（１）

解説：まずは問題文の条件を図示して考える。一相あたりの対地静電容量はC[F]なので、図１のように三相ともC[F]を介して地面と繋がる。

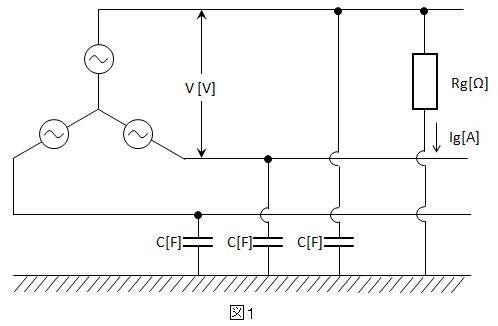
また、地絡抵抗Rg[Ω]で、一線地絡事故なので、任意の一相より地絡抵抗Rg[Ω]を介して地面と繋がる。すると図２のように一線地絡の相とそれ以外の二相間で閉回路が完成して電流が流れる。

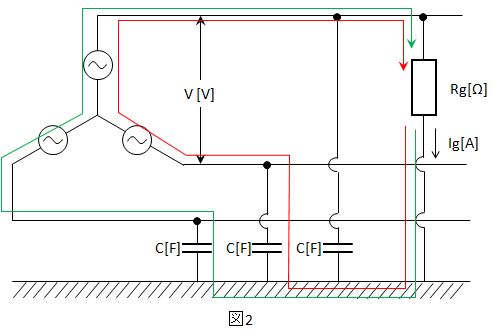
この二回路に流れる電流の和が地絡電流Igとなる。回路構成が複雑なので、テブナンの定理①のように、テブナンの定理を利用して解いていく。

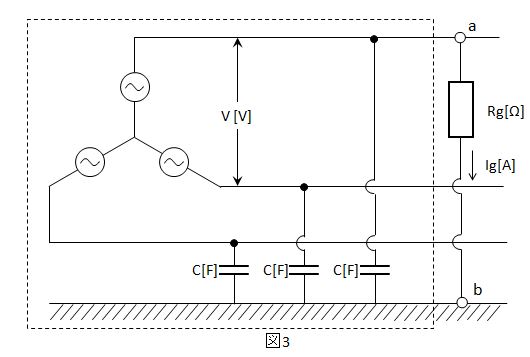
図３のように端子a,bから見た破線内の内部インピーダンスは電圧源を短絡して考えるので、静電容量C[F]３つの並列回路と考えられるので、 $Z = \frac{1}{j ω (3 C)} = - j \frac{1}{3 ω C}$

端子a,bから見た開放電圧は、一相あたりの対地電圧なので、 $E = \frac{V}{\sqrt{3}}$ [V]

したがって、テブナンの定理①より、 $I = \frac{E}{Z + R}$

ここで、 $Z + R = - j \frac{1}{3 ω C} + R g$ の大きさは $\sqrt{{R_{g}}^{2} + (\frac{1}{3 ω C})^{2}}$ であるので、

|I|= $\frac{\frac{V}{\sqrt{3}}}{\sqrt{{R_{g}}^{2} + (\frac{1}{3 ω c})^{2}}} = \frac{V}{\sqrt{3} \times \sqrt{{R_{g}}^{2} + (\frac{1}{3 ω c})^{2}}}$ ここで、 $ω = 2 π f$ なので、|I|= $\frac{V}{\sqrt{3} \times \sqrt{{R_{g}}^{2} + (\frac{1}{6 π f c})^{2}}}$

問題を選ぶ