電流による磁界の発生,磁束密度の関係　解答

正解：（２）

解説：磁束密度は透磁率と電界の大きさの積で表すので、B=μHとなる。

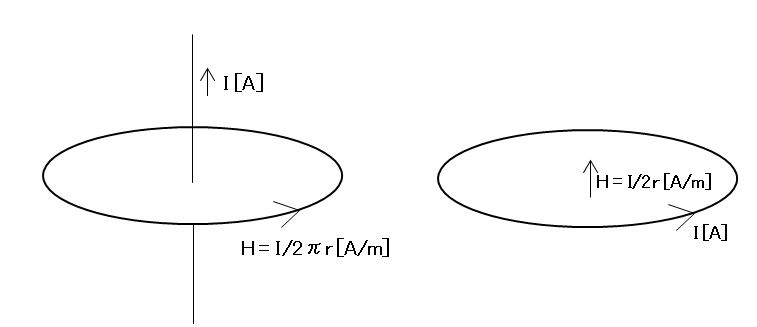
また、図のように無限長導体周りで距離r[m]だけ離れたところでの磁界の大きさは $\frac{I}{2 π r} [A / m]$ であり、その向きは右ネジの法則に従う（右ネジの進行方向に電流が流れる時、右ネジの回転方向が磁界の向き）。半径r[m]の1巻円形コイルの中心に出来る磁界の大きさは $\frac{I}{2 r} [A / m]$ となる。いずれも、ビオサバールの式（微小距離に電流Iが流れるときにr[m]離れた場所での電界の大きさは $\frac{I}{4 π r^{2}} [A / m]$ ）を利用して積分して導出出来るが、よく使う公式なので、 $\frac{I}{2 π r} [A / m]$ と $\frac{I}{2 r} [A / m]$ はそのまま覚えてしまうと便利である。

問題を選ぶ