電力計について、次の(a)及び(b)の問いに答えよ。
(a)次の文章は、電力計の原理に関する記述である。
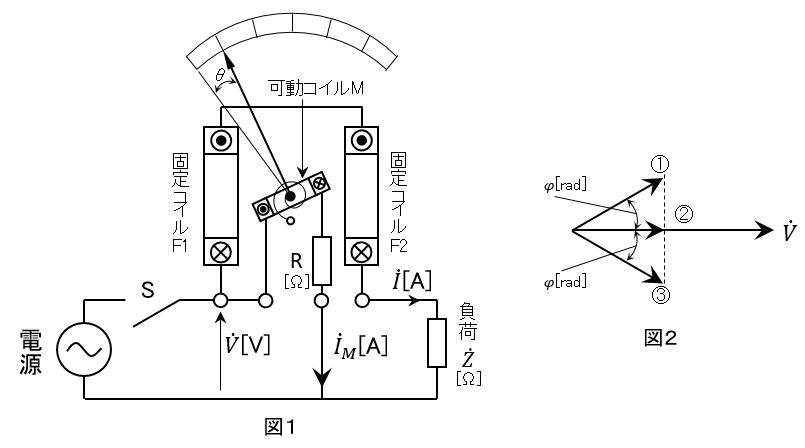
図1に示す電力計は、固定コイルF1,F2に流れる負荷電流$\dot{I}$[A]による磁界の強さと、可動コイルMに流れる電流$\dot{I}_M$[A]の積に比例したトルクが可動コイルに生じる。したがって、指針の振れ角θは(ア)に比例する。
このような形の計器は、一般に(イ)計器といわれ、(ウ)の測定に使用される。
負荷$\dot{Z}$[Ω]が誘導性の場合、電圧$\dot{V}$[V]のベクトルを基準に負荷電流$\dot{I}$[A]のベクトルを描くと、図2に示すベクトル①、②、③のうち(エ)のように表される。ただし、φ[rad]は位相角である。
上記の記述中の空白箇所(ア)、(イ)、(ウ)及び(エ)に当てはまる組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
| ア | イ | ウ | エ | |
| (1) | 負荷電力 | 電流力計形 | 交流 | ③ |
| (2) | 電力量 | 可動コイル形 | 直流 | ② |
| (3) | 負荷電力 | 誘導形 | 交流直流両方 | ① |
| (4) | 電力量 | 可動コイル形 | 交流直流両方 | ② |
| (5) | 負荷電力 | 電流力計形 | 交流直流両方 | ③ |
(b)次の文章は、図1で示した単相電力計を2個使用し、三相電力を測定する2電力計法の理論に関する記述である。
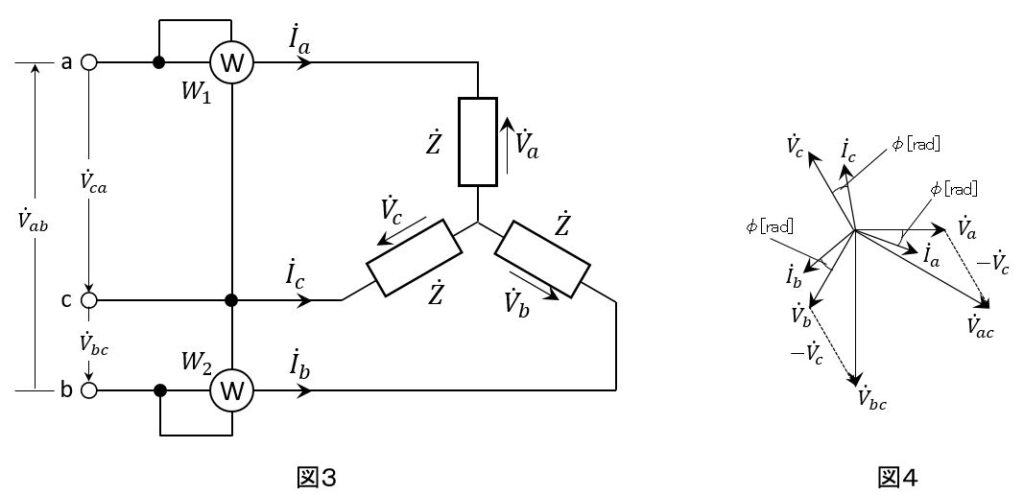
図3のように、誘導性負荷$\dot{Z}$を3個接続した平衡三相負荷回路に対称三相交流電源が接続されている。ここで、線間電圧を$\dot{V_{ab}}[V],\dot{V_{bc}}[V],\dot{V_{ca}}[V]$、負荷の相電圧を$\dot{V_{a}}[V],\dot{V_{b}}[V],\dot{V_{c}}[V]$、線電流を$\dot{I_{a}}[A],\dot{I_{b}}[A],\dot{I_{c}}[A]$で示す。
この回路で、図のように単相電力計W1とW2を接続すれば、平衡三相負荷の電力が、2個の単相電力計の指示の和として求めることができる。
単相電力計W1の電圧コイルに加わる電圧$\dot{V_{ac}}$は図4のベクトル図から$\dot{V_{ac}}=\dot{V_{a}}-\dot{V_{c}}$となる。また、単相電力計W2の電圧コイルに加わる電圧$\dot{V_{bc}}$は$\dot{V_{bc}}$=(オ)となる。
それぞれの電流コイルに流れる電流$\dot{I_{a}},\dot{I_{b}}$と電圧の関係は図4のようになる。図4におけるφ[rad]は相電圧と線電流の位相角である。
線間電圧の大きさをVab= Vbc= Vca= V[V]、線電流の大きさをIa= Ib= Ic= I[A]とおくと、単相電力計W1及びW2の指示をそれぞれP1[W],P2[W]とすれば、
P1= Vca Iacos(カ)[W]
P2= Vbc Ibcos(キ)[W]
したがって、P1とP2の和P[W]は、
P= P1+P2=VI(ク)cosφ=$\sqrt{3}$VIcosφ[W]
となるので、2個の単相電力計の指示の和は三相電力に等しくなる。
上記の記述中の空白箇所(オ)、(カ)、(キ)及び(ク)に当てはまる組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
| オ | カ | キ | ク | |
| (1) | $\dot{V_{b}}-\dot{V_{c}}$ | $\frac{π}{6}-φ$ | $\frac{π}{6}+φ$ | $2cos\frac{π}{6}$ |
| (2) | $\dot{V_{c}}-\dot{V_{b}}$ | $φ-\frac{π}{6}$ | $\frac{π}{6}+φ$ | $2sin\frac{π}{6}$ |
| (3) | $\dot{V_{b}}-\dot{V_{c}}$ | $\frac{π}{6}-φ$ | $\frac{π}{6}+φ$ | $2cos\frac{π}{3}$ |
| (4) | $\dot{V_{b}}-\dot{V_{c}}$ | $\frac{π}{3}-φ$ | $\frac{π}{3}+φ$ | $2cos\frac{π}{6}$ |
| (5) | $\dot{V_{c}}-\dot{V_{b}}$ | $\frac{π}{3}-φ$ | $\frac{π}{3}+φ$ | $2sin\frac{π}{3}$ |