次の文章は、真空中における電子の運動に関する記述である。
図のようにx軸上の負の向きに大きさが一定の電界E[V/m]が存在しているとき、
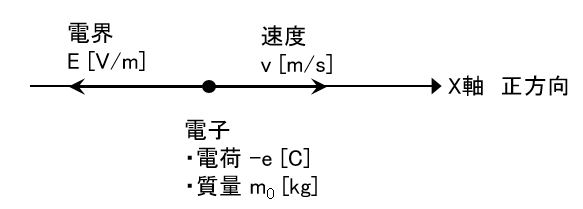
x軸上に電荷が-e[C](eは電荷の絶対値)、質量m0[kg]の1個の電子を置いた場合を考える。x軸上の正方向の電子の加速度をa[m/s2]とし、また、この電子に加わる力の正方向をx軸の正方向にとったとき、電子の運動方程式はm0a=(ア)・・・①
となる。①式から電子は等加速度運動をすることがわかる。したがって、電子の初速度を零としたとき、x軸の正方向に向かう電子の速度v[m/s]は時間t[s]の(イ)関数となる。また、電子の走行距離xdis[m]は時間t[s]の(ウ)関数で表される。さらに、電子の運動エネルギーは時間t[s]の(エ)で増加することがわかる。ただし、電子の速度v[m/s]はその質量の変化が無視できる範囲とする。
上記の記述中の空白箇所(ア)、(イ)、(ウ)、(エ)に当てはまる組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
| ア | イ | ウ | エ | |
| (1) | eE | 一次 | 二次 | 1乗 |
| (2) | $\frac{1}{2}$eE | 二次 | 一次 | 1乗 |
| (3) | eE2 | 一次 | 二次 | 2乗 |
| (4) | $\frac{1}{2}$eE | 二次 | 一次 | 2乗 |
| (5) | eE | 一次 | 二次 | 2乗 |